vasttastic.blogg.se - Supplementary angle pictures

The supplement of an angle is obtained by subtracting it from 180 degrees. What Angle is Supplementary to 84 Degrees? The definition of supplementary angles holds true only for two angles. Though the sum of angles, 40°, 90° and 50° is 180°, they are not supplementary angles because supplementary angles always occur in pairs. No, three angles can never be supplementary even though their sum is 180 degrees. Two angles form a pair of complementary angles when their sum is 90°, whereas, two angles form a pair of supplementary angles when their sum is 180°. No, supplementary and complementary angles are not the same.

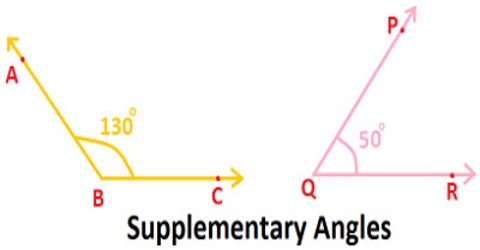
Are Supplementary and Complementary Angles the Same? Yes, two right angles are always supplementary because 90° + 90° = 180°. Can Two Right angles be Supplementary Angles? If two obtuse angles are put together, their sum will always be greater than 180°, so two obtuse angles can never be supplementary angles. No, if two angles are supplementary, then they are both either right angles or one of them is acute and one of them is obtuse. Can Two Obtuse Angles be Supplementary Angles? If two acute angles are put together, their sum will always be less than 180°, so two acute angles can never be supplementary angles. Can Two Acute Angles be Supplementary Angles? Supplementary angles always form a straight angle (180 degrees) when they are put together. For example, if ∠A + ∠B = 180°, then ∠A and ∠B are called supplementary angles. In geometry, two angles are said to be supplementary angles if they add up to 180 degrees.

"C" is for "Complementary" and "C" is for "Corner." Hence, you can remember that two "Complementary" angles when put together form a "Corner (right)" angle.įAQs on Supplementary Angles What are Supplementary Angles in Geometry?.

"S" is for "Supplementary" and "S" is for "Straight." Hence, you can remember that two "Supplementary" angles when put together form a "Straight" angle.

Here is a short trick for you to understand the difference between supplementary angles and complementary angles. Tips on Supplementary angles vs Complementary angles Two angles are said to be supplementary if they add up to 180 degrees. Two angles are said to be complementary if they add up to 90 degrees. The supplementary vs complementary angles table. The following table shows the difference between supplementary and complementary angles. These angles have numerous real-time applications, the most common being the crossroads. While supplementary angles add up to 180 °, complementary angles add up to 90°.

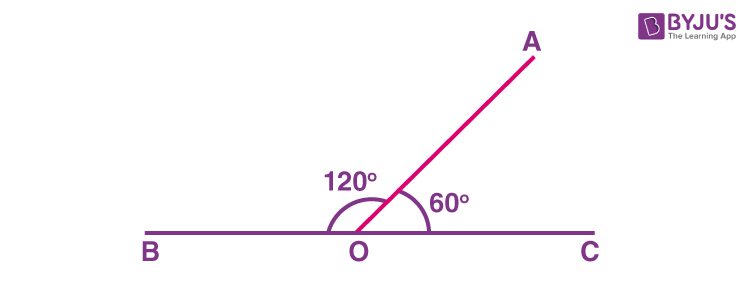
Supplementary and complementary angles are those angles that exist in pairs. Non-adjacent supplementary angles, when put together, form a straight angle. Hence, these two angles are non-adjacent supplementary angles. They also add up to 180 degrees, that is, ∠ABC+ ∠PQR = 79 ° + 101 ° = 180 °. Here, ∠ABC and ∠PQR are non-adjacent angles as they neither have a common vertex nor a common arm. Two supplementary angles that are NOT adjacent are said to be non-adjacent supplementary angles. Hence, these two angles are adjacent supplementary angles. They also add up to 180 degrees, that is, ∠COB + ∠ AOB = 70 ° + 110 ° = 180 °. Here, ∠COB and ∠AOB are adjacent angles as they have a common vertex, O, and a common arm OB.

Two supplementary angles with a common vertex and a common arm are said to be adjacent supplementary angles. Each of these types of supplementary angles is explained below. So, there are two types of supplementary angles. Supplementary angles can either be adjacent or non-adjacent. Adjacent and Non-Adjacent Supplementary Angles